走向现代数学学术报告 - 薛文东博士（No. 676）

题目：Convergence analysis of numerical methods for the compressible Navier-Stokes system

报告人：薛文东 博士（中国科学院数学与系统科学研究院）

时间：2023年12月18日，9:30

地点：东海岸校区E教340

摘要：This talk consists of two main parts. Firstly, we investigate the convergence analysis of a mixed discontinuous Galerkin-finite element method for the three-dimensional compressible Navier-Stokes system. For the adiabatic coefficients , the construction of weak solutions to compressible Navier-Stokes system via our numerical scheme is rigorously established by compactness arguments and the discrete Lions-Feireisl existence theory. For the whole range of adiabatic coefficients , the new error estimate of this scheme is proved by the discrete relative entropy method, where the convergence rate of the relative energy in the -norm is . Moreover, the Low Mach asymptotic preserving error between a discrete solution of this scheme and the strong solution of the incompressible Navier-Stokes system is derived, where the uniform convergence rate is 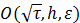. All convergence results are unconditional in the sense that we do not require the boundedness of the numerical solution and the CFL condition. Secondly, an interesting question is to go further and prove the convergence and error estimates of this scheme for the isothermal system, and derive the uniform convergence rate of a low Mach asymptotic preserving numerical scheme for the isentropic system, and establish the unconditional error estimate of a helicity-conserving implicit MAC scheme for some compressible viscous flow models.

报告人简介：薛文东，博士毕业于中国科学院数学与系统科学研究院，师从毛士鹏研究员；目前在科学与工程计算国家重点实验室做访问学者。主要研究方向是计算流体力学与多物理场数值计算、可压缩Navier-Stokes系统/可压缩Euler系统/可压缩MHD系统保结构算法和渐近保持格式，以及解的适定性分析、铁磁流体动力学建模，解的适定性分析及保结构算法。在国际期刊Journal of Scientific Computing和Journal of Computational Mathematics发表了两篇SCI论文。